Hari/Tanggal : Rabu, 28 Agustus 2024
Fase /Kelas : C/5
Muatan Pembelajaran :
- Matematika : KPK dan FPB
- Pendidikan Pancasila : Sila Pancasila
- Bahasa Indonesia : Buku Jendela Dunia
Capaian Pembelajaran Matematika: Pada akhir fase C,Mereka dapat menyelesaikan masalah yang berkaitan dengan KPK dan FPB.
Capaian Pembelajaran Pend, Pancasila : Peserta didik mampu memahami kronologi sejarah kelahiran Pancasila; meneladani sikap para perumus Pancasila dan menerapkan di lingkungan masyarakat; menghubungkan sila-sila dalam Pancasila sebagai suatu kesatuan yang utuh, menguraikan makna nilai-nilai Pancasila sebagai dasar negara, pandangan hidup, dan ideologi bangsa dan negara.
Capaian Pembelajaran Bahasa Indonesia
1. Elemen Membaca
Pada akhir fase C, peserta didik memiliki kemampuan berbahasa untuk berkomunikasi dan bernalar sesuai dengan tujuan dan konteks sosial. Peserta didik menunjukkan minat terhadap teks, mampu memahami, mengolah, dan menginterpretasi informasi dan pesan dari paparan lisan dan tulis tentang topik yang dikenali dalam teks narasi dan informatif. Peserta didik mampu menanggapi dan mempresentasikan informasi yang dipaparkan; berpartisipasi aktif dalam diskusi; menuliskan tanggapannya terhadap bacaan menggunakan pengalaman dan pengetahuannya; menulis teks untuk menyampaikan pengamatan dan pengalamannya dengan lebih terstruktur. Peserta didik memiliki kebiasaan membaca untuk hiburan, menambah pengetahuan, dan keterampilan.
Assalamualaikum wr.wb
Apa kabar anak sholih/Sholihah?
Sudah siap belajar hari ini ?
Sebelum belajar kita jangan lupa berdoa terlebih dahulu yaa.
Pendidikan Pancasila
Pancasila diumpamakan sebagai satu paket lengkap yang menopang Negara Kesatuan Republik Indonesia. Pancasila merupakan satu kesatuan yang bulat dan utuh dari kelima silanya. Sila kesatu menjiwai sila kedua, menjiwai sila ketiga, keempat, dan kelima. Sila kedua dijiwai oleh sila
kesatu, ketiga, keempat, dan kelima, dan begitu seterusnya. Kelima sila tidak bisa dilepas satu dengan yang lainnya. Walaupun masing-masing sila mempunyai nilai-nilai sendiri tetapi hubungan antarsila merupakan hubungan yang utuh dan saling terkait.
Setiap sila yang membentuk Pancasila merupakan unsur yang mutlak yang membentuk kesatuan, bukan unsur pelengkap. Artinya satu sila menjiwai dan dijiwai oleh sila-sila yang lain. Sila Pertama menjiwai sila kedua, ketiga, keempat, dan kelima, dan demikian seterusnya. Misalnya, meskipun Sila Ketuhanan Yang Maha Esa merupakan sila yang berkaitan dengan Tuhan, tetapi tidak berarti sila-sila yang lain hanya sebagai pelengkap saja.
Setiap sila yang membentuk Pancasila juga sebagai satu kesatuan yang mutlak, tidak dapat ditambah dan dikurangi. Oleh karena itu, Pancasila tidak dapat diubah menjadi Trisila atau ekasila.
Kerjakan latihan berikut!
1. Sila kedua Pancasila "Kemanusiaan yang adil dan beradab" disimbolkan dengan "Rantai" berwarna emas. Penerapan makna simbol "Rantai" dalam kehidupan sehari-hari salah satunya adalah ....
a. Membantu teman yang sedang dalam kesulitan
b. Membuang sampah pada tempatnya
c. Melaksanakan ibadah tepat waktu
d. Menjahili teman
2. Setiap hari Senin warga sekolah melaksanakan upacara bendera sebagai. wujud nasionalisme dan patriotisme. hal di atas merupakan pencerminan dari sila ....
a. Kesatu
b. Kedua
c. Ketiga
d. Keempat
3. Kegiatan yang sesuai dengan penerapan sila Pancasila yang berbunyi "Persatuan Indonesia" adalah ....
a. Berdoa menurut agama dan kepercayaan masing-masing
b. Memberi sedekah kepada fakir miskin
c. Melaksanakan upacara setiap hari senin
d. Membuang sampah pada tempatnya
4.Menghargai hak asasi menusia merupakan nilai-nilai Pancasila sila .....
a. Kesatu
b. Kedua
c. Ketiga
d. Keempat
5. Mengerjakan piket kelas merupakan pengamalan Pancasila sila ....
a. Kesatu
b. Kedua
c. Ketiga
d. keempat
Matematika
Menentukan KPK Dua Bilangan atau Lebih
KPK atau Kelipatan Persekutuan Terkecil adalah bilangan bulat positif dengan nilai terkecil yang bisa habis bila dibagi dengan kedua bilangan tersebut Untuk menentukan KPK dua buah bilangan dapat dilakukan dengan menggunakan faktorisasi prima dan kelipatan bilangan. Perhatikan beberapa contoh berikut ini
1. Menggunakan Kelipatan Kedua Bilangan
Kelipatan bilangan adalah bilangan-bilangan yang merupakan hasil kali bilangan tersebut dengan bilangan bulat positif. Kelipatan bilangan dapat digunakan untuk menentukan KPK dua bilangan atau lebih. Perhatikan contoh soal berikut ini !
Berapakah KPK dari 4 dan 6?
Penyelesaian
Kelipatan 4 adalah 4, 8, 12, 16, 20, 24, 28, 32, 40, …
Kelipatan 6 adalah 6, 12, 18, 24, 30, 36, …
Kelipatan persekutuan dari 4 dan 6 adalah 12, 24, …
Jadi, KPK dari 4 dan 6 adalah 12.
2. Menggunakan Pohon Faktor
Pohon faktor merupakan deretan pembagian yang turun kebawah dengan menggunakan pembagian menggunakan bilangan prima. Cara menentukan KPK dua bilangan atau lebih dapat dilakukan dengan langkah-langkah sebagai berikut :
- Tulislah bilangan-bilangan tersebut dalam bentuk perkalian faktor prima.
- Ambil semua faktor yang sama dari bilangan-bilangan tersebut.
- Apabila faktor yang sama tersebut memiliki pangkat yang berbeda, maka ambil faktor yang pangkatnya terbesar.
Berapakah KPK dari 4 dan 6?
Penyelesaian
Faktorisasi prima dari 4 = 2²
Faktorisasi prima dari 6 = 2 × 3
Jadi KPK 4 dan 6 adalah = 2² x 3 = 4 x 3 = 12
B. Menentukan FPB Dua Bilangan atau Lebih
1. Menggunakan Faktor Persekutuam
Faktor persekutuan merupakan bilangan faktor yang sama dari dua bilangan atau lebih. FPB diambil dari faktor yang memiliki nilai terbesar.. Perhatkan contoh soal berikut ini!
Carilah FPB dari 6, 9, dan 18 ...
Pembahasan
Faktor dari 6 adalah = {1, 2, 3, 6}
Faktor dari 9 adalah = {1, 2, 3, 9}
Faktor dari 18 adalah = {1, 2, 3, 6, 9, 18}
Faktor persekutuan dari ketiga bilangan tersebut adalah 1, 2, 3
Nilai terbesar dari faktor tersebut adalah 3 maka FPB dari 6, 9, dan 18 adalah 3
2. Menggunakan Pohon Faktor
Pohon faktor merupakan deretan pembagian yang turun kebawah dengan menggunakan pembagian menggunakan bilangan prima. Cara menentukan FPB menggunakan phon faktor adalah sebagai berikut !
- Tulislah bilangan-bilangan tersebut ke dalam bentuk perkalian faktor prima.
- Setelah itu ambillah faktor yang sama dari bilangan-bilangan tersebut.
- Apabila faktor yang sama tersebut memiliki pangkat yang berbeda, maka ambillah faktor yang memiliki nilai pangkat terkecil.
Perhatikan contoh soal berikut ini !
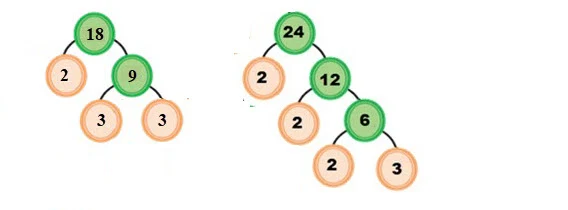
Tentukan FPB dari 18 dan 24
Pembahasan :
Faktor 18 = 2 x 3 x 3 = 2 x 3²
Faktor 24 = 2 x 2 x 2 x 3 = 2³ x 3
FPB = 2 x 3 = 6
Jadi FPB dari 18 dan 24 adalah 6
Ayo Mencoba
1. Tentukan pohon faktor setiap pasangan bilangan berikut.
a. 6 dan 9
b. 9 dan 12
c. 20 dan 30
d. 32 dan 48
e. 12 dan 18
2. Tentukan KPK dua bilangan berikut dengan menggunakan faktorisasi prima.
a. 10 dan 12
Faktorisasi prima dari 10 = 2 × 5
Faktorisasi prima dari 12 = 2² × 3
Maka KPKnya = 2² x 3 x 5 = 4 x 3 x 5 = 60
b. 15 dan 20
Faktorisasi prima dari 15 = 3 × 5
Faktorisasi prima dari 20 = 2² x 5
Maka KPKnya = 2² × 3 × 5 = 4 × 3 × 5 = 60
e. 18 dan 20
Faktorisasi prima dari 18 = 2 x 3²
Faktorisasi prima dari 20 = 2² x 5
Maka KPKnya = 2² x 3² x 5 = 4 × 9 × 5 = 180
d. 42 dan 54
Faktorisasi prima dari 42 = 2 x 3 × 7
Faktorisasi prima dari 54 = 2 x 3³
Maka KPKnya = 2 x 3³ x 7 = 2 × 27 × 7 = 378
e. 38 dan 40
Faktorisasi prima dari 38 = 2 x 19
Faktorisasi prima dari 40 = 2³ × 5
Maka KPKnya = 2³ × 5 × 19 = 8 × 5 × 19 = 760
3. Tentukan KPK tiga bilangan berikut dengan menggunakan faktorisasi prima.
a. 6, 8 dan 9
Faktorisasi prima :
6 = 2 × 3
8 = 2³
9 = 3²
KPK = 2³ × 3² = 8 × 9 = 72
Jadi KPK dari bilangan 6, 8 , dan 9 adalah 72.
b. 9, 10 dan 12
Faktorisasi prima :
9 = 3²
10 = 2 × 5
12 = 2² × 3
KPK = 2² × 3² × 5 = 4 × 9 × 5 = 180
Jadi KPK dari bilangan 9, 10, dan 12 adalah 180.
c. 12, 16 dan 18
Faktorisasi prima :
12 = 2² × 3
16 = 2⁴
18 = 2 × 3²
KPK = 2⁴ × 3² = 16 × 9 = 144
Jadi KPK dari bilangan 12, 16, dan 18 adalah 144.
d. 15, 20 dan 30
Faktorisasi prima :
15 = 3 × 5
20 = 2² × 5
18 = 2 × 3 × 5
KPK = 2² × 3 × 5 = 4 × 3 × 5 = 60
Jadi KPK dari bilangan 15, 20, dan 30 adalah 60.
e. 32, 36 dan 48
Faktorisasi prima :
32 = 2⁵
36 = 2² × 3²
48 = 2⁴ × 3
KPK = 2⁵ × 3² = 32 × 9 = 288
Jadi KPK dari bilangan 32, 36, dan 48 adalah 288.
A. Menentukan FPB Dua Bilangan
Faktor persekutuan adalah faktor yang sama dari dua bilangan atau lebih.
Ayo Mencoba
1. Tentukan FPB dua bilangan berikut dengan menggunakan faktor persekutuan.
a. 6 dan 9
Faktor 6 = 1, 2, 3, 6
Faktor 9 = 1, 3, 9
Faktor persekutuan dari 6 dan 9 = 1 , dan 3
FPB dari 6 dan 9 = 3
b. 9 dan 12
Faktor 9 = 1, 3, 9
Faktor 12 = 1, 2, 3, 4, 6, 12
Faktor persekutuan dari 9 dan 12 = 1 , dan 3
FPB dari 9 dan 12 = 3
c. 12 dan 18
Faktor 12 = 1, 2, 3, 4, 6, 12
Faktor 18 = 1, 2, 3, 6, 9, 18
Faktor persekutuan dari 12 dan 18 = 1, 2 , 3, dan 6
FPB dari 12 dan 18 = 6
d. 20 dan 30
Faktor 20 = 1, 2, 4, 5, 10, 20
Faktor 30 = 1, 2, 3, 5, 6, 10, 15, 30
Faktor persekutuan dari 20 dan 30 = 1, 2, 5, dan 10
FPB dari 20 dan 30 = 10
e. 32 dan 48
Faktor 32 = 1, 2, 4, 8, 16, 32
Faktor 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Faktor persekutuan dari 32 dan 48 = 1, 2, 4 , 8, dan 16
FPB dari 32 dan 48 = 16
2. Tentukan FPB dua bilangan berikut dengan menggunakan faktorisasi prima.
a. 10 dan 12
Faktorisasi 10 = 2 × 5
Faktorisasi 12 = 2² × 3
FPB ditentukan berdasarkan faktor prima yang sama dari kedua bilangan dengan pangkat terendah.
Jadi FPB dari 10 dan 12 adalah 2
b. 15 dan 20
Faktorisasi 5 = 3 × 5
Faktorisasi 20 = 2² × 5
FPB ditentukan berdasarkan faktor prima yang sama dari kedua bilangan dengan pangkat terendah.
Jadi FPB 15 dan 20 adalah 5
c. 18 dan 20
Faktorisasi 18 = 2 × 3²
Faktorisasi 20 = 2² × 5
FPB ditentukan berdasarkan faktor prima yang sama dari kedua bilangan dengan pangkat terendah.
Jadi FPB 18 dan 20 adalah = 2
d. 38 dan 40
Faktorisasi 38 = 2 × 19
Faktorisasi 40 = 2³ × 5
FPB ditentukan berdasarkan faktor prima yang sama dari kedua bilangan dengan pangkat terendah.
Jadi FPB dari 38 dan 40 adalah = 2
e. 42 dan 54
Faktorisasi 42 = 2 × 3 × 7
Faktorisasi 54 = 2 × 3³
FPB ditentukan berdasarkan faktor prima yang sama dari kedua bilangan dengan pangkat terendah.
Jadi FPB dari 42 dan 54 adalah = 2 × 3 = 6
3. Tentukan FPB tiga bilangan berikut dengan menggunakan faktor persekutuan.
a. 6, 8 dan 9
Faktor 6 = 1, 2, 3, 6
Faktor 8 = 1, 2, 4, 8
Faktor 9 = 1, 3, 9
Faktor persekutuan dari 6, 8 dan 9 = 1
FPB dari 6, 8 dan 9 = 1
b. 9, 10 dan 12
Faktor 9 = 1, 3, 9
Faktor 10 = 1, 2, 5, 10
Faktor 12 = 1, 2, 3, 4, 6, 12
Faktor persekutuan dari 9, 10 dan 12 = 1
FPB dari 9, 10 dan 12 = 1
c. 12, 16 dan 18
Faktor 12 = 1, 2, 3, 4, 6, 12
Faktor 16 = 1, 2, 4, 8, 16
Faktor 18 = 1, 2, 3, 6, 9, 18
Faktor persekutuan dari 12, 16 dan 18 = 1, 2
FPB dari 12, 16 dan 18 = 2
d. 15, 20 dan 30
Faktor 15 = 1, 3, 5, 15
Faktor 20 = 1, 2, 4, 5, 10, 20
Faktor 30 = 1, 2, 3, 5, 6, 10, 15, 30
Faktor persekutuan dari 15, 20 dan 30 = 1, 5
FPB dari 15, 20 dan 30 = 5
e. 32, 36 dan 48
Faktor 32 = 1, 2, 4, 8, 16, 32
Faktor 36 = 1, 2, 3, 4, 6, 9, 12, 18, 36
Faktor 48 = 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Faktor persekutuan dari 32, 36 dan 48 = 1, 2, 4
FPB dari 32, 36 dan 48 = 4
Bahasa Indonesia
Pilihlah huruf a, b, c, atau d di depan jawaban yang paling tepat!
Perhatikan cerita berikut! (Untuk menjawab soal nomor 1 - 4)
Gajah dan Semut
Suatu hari, kawanan gajah yang besar datang ke hutan untuk mencari makan. Kehadiran gajah ini
mengganggu kawanan semut yang tinggal di sana. Banyak rumah semut hancur karena diinjak
gajah yang mencari makan.
"Pergilah dari sini, gajah! Ini daerah tempat kami tinggal," kata salah satu semut.
Mendengar ucapan itu, gajah hanya tertawa. Ia tak peduli dan menganggap semut adalah
binatang kecil yang tidak berbahaya.
Kawanan semut merasa kesal dan berencana untuk mengusir gajah-gajah itu dari hutan tempat
mereka tinggal. Keesokan harinya, semut-semut mencoba bicara pada kawanan gajah dan
meminta mereka meninggalkan hutan.
Gajah menolak untuk meninggalkan hutan dan hal ini membuat kawanan semut semakin marah.
Semut-semut itu pun menyerang kawasan gajah dengan menggigit kulit dan masuk ke dalam
telinga hingga gajah-gajah terjatuh. Kawanan gajah akhirnya menyerah dan meninggalkan hutan.
Mereka sadar bahwa semut-semut itu tidak bisa diremehkan hanya karena memiliki badan
kecil.
Soal No.1
Tema berikut yang sesuai dengan cerita di atas yaitu ...
A.keluarga
B.persahabatan
C.perjuangan
D.pertualangan
Soal No.2
Salah satu tokoh dalam cerita di atas adalah semut. Sifat tokoh semut yaitu ....
A.bijaksana
B.sombong
C.rendah diri
D.pemberani
Soal No.3
Latar tempat dari cerita di atas yaitu di ....
A.hutan
B.sawah
C.pegunungan
D.kebun binatang
Soal No.4
Amanat yang dapat kita pelajari dari cerita di atas yaitu ....
A.kita harus saling tolong menolong
B.tidak meremehkan orang lain
C.tidak boleh iri hati dan dengki
D.selalu menuruti nasihat orang tua
Soal No.5
Berikut ini salah satu unsur intrinsik cerita yaitu ....
A.penulis cerita
B.aliran cerita
C.alur cerita
D.riwayat cerita
Alhamdulillah untuk pertemuan hari ini kalian telah mengikutinya dengan baik.
Apakah anak-anak bahagia belajar hari ini? Apakah anak-anak nyaman belajar hari ini? Apa yang telah kalian pelajari hari ini?
Alhamdulillah jika anak-anak sudah memahami materi hari ini dengan perasaan yang bahagia.
Terimakasih atas kerjasamanya jangan lupa sholat lima waktu dan murojaah dirumah
Ibu guru akhiri, Wassalamu’alaikum Wb
Kesimpulan : Alhamdulillah kegiatan belajar hari ini berjalan dengan lancar dan anak mampu mengerjakan KPK dengan menggunakan kelipatan dan ada beberapa peserta didik yang mengalami kesulitan menentukan dengan faktorisasi prima





Tidak ada komentar:
Posting Komentar