Tema 7 : Peristiwa dalam kehidupan
Subtema 2 : Peristiwa kebangsaan seputar proklamasi
Pembelajaran : 2
Muatan Pembelajaran :
1. SBdP : Pola lantai pada gerak tari kreasi daerah
2. B. Indonesia : Mengemukakan informasi penting pada teks narasi sejarah
3. IPA : Faktor yang mempengaruhi perubahan wujud benda
Assalamu'alaikum warohmatullahi wabarokatuh
Anak
sholeh sholehah, apa kabarnya hari ini ? semoga selalu sehat, semangat
dan ceria serta selalu dalam lindungan Allah SWT. anak anak yang sholeh
dan sholehah, berikut ini materi yang akan kita pelajari hari ini :
Tujuan Pembelajaran :
- Siswa mengetahui Pola lantai pada gerak tari kreasi daerah
- Siswa mampu Mengemukakan informasi penting pada teks narasi sejarah
- Siswa mengetahui Faktor yang mempengaruhi perubahan wujud benda
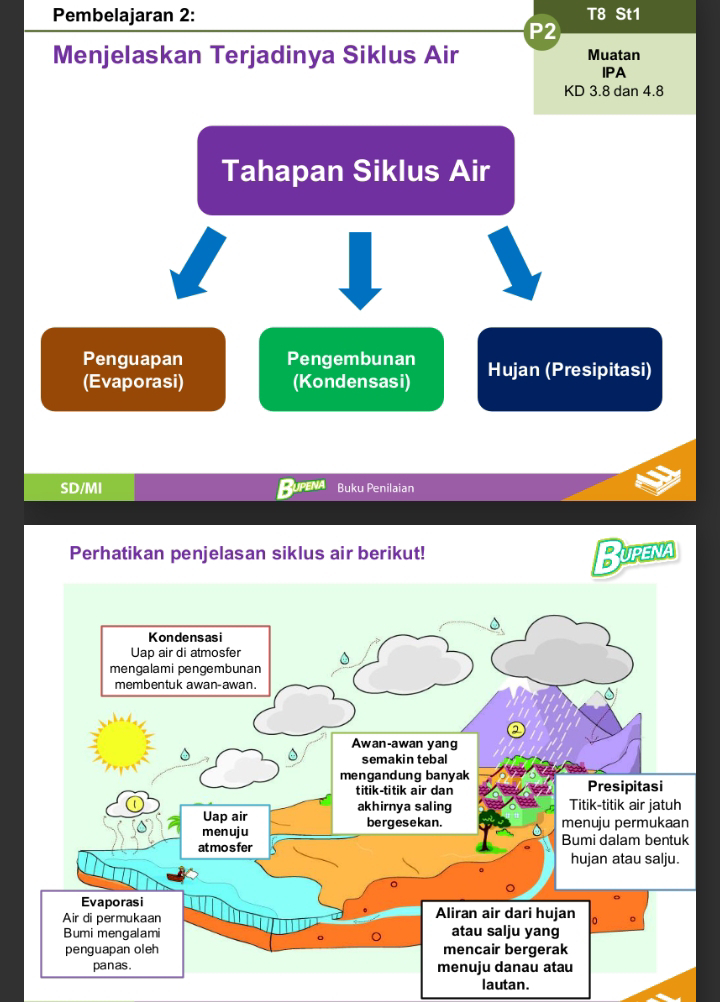
Perhatikan rangkuman materi hari ini :
Tema 7 : Peristiwa dalam kehidupan
Subtema 2 : Peristiwa kebangsaan seputar proklamasi
Pembelajaran : 1 dan MTK
Muatan Pembelajaran :
1. IPS : Peristiwa Penting Seputar Proklamasi
2. B. Indonesia : Mengelompokkann informasi teks narasi sejarah dengan peta pikiran
3. IPA : Perubahan wujud benda yang dapat kembali
4. MTK : Bangun Ruang
Assalamu'alaikum warohmatullahi wabarokatuh
Anak
sholeh sholehah, apa kabarnya hari ini ? semoga selalu sehat, semangat
dan ceria serta selalu dalam lindungan Allah SWT. anak anak yang sholeh
dan sholehah, berikut ini materi yang akan kita pelajari hari ini :
Tujuan Pembelajaran :
- Siswa mengetahui Peristiwa Penting Seputar Proklamasi
- Siswa mampu Mengelompokkann informasi teks narasi sejarah dengan peta pikiran
- Siswa mengetahui Perubahan wujud benda yang dapat kembali
- Siswa mampu menghitung volume bangun ruang
Perhatikan rangkuman materi hari ini :



Rumus dan Cara Mencari Volume Bangun Ruang
1. Kubus
Rumus mencari volume kubus adalah V = r³ atau V = r x r x r
Keterangan:
r = panjang rusuk kubus
Contoh soal mencari volume kubus:
Sebuah kubus diketahui memiliki panjang rusuk 10 cm. Berapakah volume kubus tersebut?
Jawaban:
Diketahui r = 10 cm
V = r³
V = 10³
Volume kubus tersebut yaitu 1000 cm³
2. Balok
Rumus volume balok ialah V = P x L x T.
Keterangan:
P = Panjang
L = Lebar
T = Tinggi.
Contoh soal:
Andi menemukan sebuah balok berukuran panjang 8 cm, lebar 6 cm, dan tinggi 5 cm. Berapa volume balok tersebut?
Jawaban:
Cara mencari volume bangun ruang ini mudah, kita bisa langsung memasukkan angka ke dalam rumusnya.
V = P x L x T
V = 8 x 6 x 5
Volume kubus = 240 cm³
3. Bola
Rumus mencari volume bola yaitu V = 4/3 x π × r³
Keterangan:
π = 22/7 atau 3,14
r = ukuran jari-jari
Contoh soal mencari volume bola:
Nani mendapat hadiah bola dari kakaknya. Berapa volume bola tersebut kalau jari-jarinya berukuran 20 cm?
Jawaban:
Rumus bangun ruang bola adalah V = 4/3 x π × r³
V = 4/3 x 3,14 × 20³
V = 4/3 x 3,14 × 8.000
Volume bola Nani adalah 33.493,3 cm³
4. Tabung
Rumus volume tabung = π × r² × t
Keterangan:
r = ukuran jari-jari lingkaran
t = tinggi
Contoh soal:
Sebuah mainan berbentuk tabung diketahui memiliki ukuran jari-jari 10 cm dan tinggi 30 cm. Berapakah volume tabung itu?
Jawaban:
Cara mencari volume bangun ruang ini sama seperti sebelumnya, langsung masukkan angka yang diketahui ke dalam rumusnya.
V = π × r² × t
V = 3,14 x 10² x 30
V = 3,14 x 100 x 30
Volume tabung tersebut yaitu 9.420 cm³
5. Kerucut
Volume kerucut = ⅓ × π × r² × t
Keterangan:
π = 22/7 atau 3,14
r = panjang jari-jari
t = tinggi kerucut
Contoh soal mencari volume kerucut:
Berapakah volume sebuah kerucut jika panjang jari-jari 10 cm dan tinggi kerucut 30 cm?
Jawaban:
Rumus volume kerucut V = ⅓ × π × r² × t
V = ⅓ × π × r² × t
V = ⅓ × 3,14 × 10² × 30
V = ⅓ × 3,14 × 100 × 30
Volume kerucut adalah 3.140 cm³
6. Limas
Volume limas = 1/3 x Luas Alas x Tinggi
Keterangan:
Luas alas sebuah limas ditentukan oleh bangun ruang yang dipakai.
Contoh soal menghitung volume limas:
Sebuah
mainan piramida berbentuk limas segiempat diketahui memiliki ukuran
panjang sisi permukaannya 10 cm dan tinggi limas 15 cm. Berapakah volume
piramida mainan tersebut?
Jawaban:
Cara mencari volume bangun ruang limas segiempat sedikit berbeda karena Anda perlu mencari ukuran luas alasnya terlebih dahulu.
V = 1/3 x Luas Alas x Tinggi
V = 1/3 x (sisi x sisi) x Tinggi
V = 1/3 x 100 x 15
V = 500 cm³
7. Prisma
Rumus mencari volume prisma yaitu V = Luas Alas x Tinggi
Keterangan:
Luas
alas dari sebuah prisma juga bisa berbeda-beda, misalnya alas segitiga
siku-siku atau segitiga sama sisi. Rumus menghitung luas alasnya pun
akan berbeda.
Contoh soal:
Sebuah prisma segitiga memiliki panjang 3 cm, lebar 5 cm, dan tinggi 10 cm. Berapakah volumenya?
Jawaban:
V = ½ x (P x L x T)
V = ½ x (3 x 5 x 10)
V = ½ x (150)
V = 75 cm³